|
| 1 | +# Levenshtein Distance |
| 2 | + |
1 | 3 | _Read this in other languages:_ |
2 | 4 | [_Tiếng Việt_](README.md) |
| 5 | + |
| 6 | +The Levenshtein distance is a string metric for measuring the |
| 7 | +difference between two sequences. Informally, the Levenshtein |
| 8 | +distance between two words is the minimum number of |
| 9 | +single-character edits (insertions, deletions or substitutions) |
| 10 | +required to change one word into the other. |
| 11 | + |
| 12 | +## Definition |
| 13 | + |
| 14 | +Mathematically, the Levenshtein distance between two strings |
| 15 | +`a` and `b` (of length `|a|` and `|b|` respectively) is given by |
| 16 | + |
| 17 | +where |
| 18 | + |
| 19 | + |
| 20 | + |
| 21 | +where |
| 22 | + |
| 23 | +is the indicator function equal to `0` when |
| 24 | + |
| 25 | +and equal to 1 otherwise, and |
| 26 | + |
| 27 | +is the distance between the first `i` characters of `a` and the first |
| 28 | +`j` characters of `b`. |
| 29 | + |
| 30 | +Note that the first element in the minimum corresponds to |
| 31 | +deletion (from `a` to `b`), the second to insertion and |
| 32 | +the third to match or mismatch, depending on whether the |
| 33 | +respective symbols are the same. |
| 34 | + |
| 35 | +## Example |
| 36 | + |
| 37 | +For example, the Levenshtein distance between `kitten` and |
| 38 | +`sitting` is `3`, since the following three edits change one |
| 39 | +into the other, and there is no way to do it with fewer than |
| 40 | +three edits: |
| 41 | + |
| 42 | +1.**k**itten → **s**itten (substitution of "s" for "k") |
| 43 | +2. sitt**e**n → sitt**i**n (substitution of "i" for "e") |
| 44 | +3. sittin → sittin**g** (insertion of "g" at the end). |
| 45 | + |
| 46 | +## Applications |
| 47 | + |
| 48 | +This has a wide range of applications, for instance, spell checkers, correction |
| 49 | +systems for optical character recognition, fuzzy string searching, and software |
| 50 | +to assist natural language translation based on translation memory. |
| 51 | + |
| 52 | +## Dynamic Programming Approach Explanation |
| 53 | + |
| 54 | +Let’s take a simple example of finding minimum edit distance between |
| 55 | +strings `ME` and `MY`. Intuitively you already know that minimum edit distance |
| 56 | +here is `1` operation, which is replacing `E` with `Y`. But |
| 57 | +let’s try to formalize it in a form of the algorithm in order to be able to |
| 58 | +do more complex examples like transforming `Saturday` into `Sunday`. |
| 59 | + |
| 60 | +To apply the mathematical formula mentioned above to `ME → MY` transformation |
| 61 | +we need to know minimum edit distances of `ME → M`, `M → MY` and `M → M` transformations |
| 62 | +in prior. Then we will need to pick the minimum one and add _one_ operation to |
| 63 | +transform last letters `E → Y`. So minimum edit distance of `ME → MY` transformation |
| 64 | +is being calculated based on three previously possible transformations. |
| 65 | + |
| 66 | +To explain this further let’s draw the following matrix: |
| 67 | + |
| 68 | +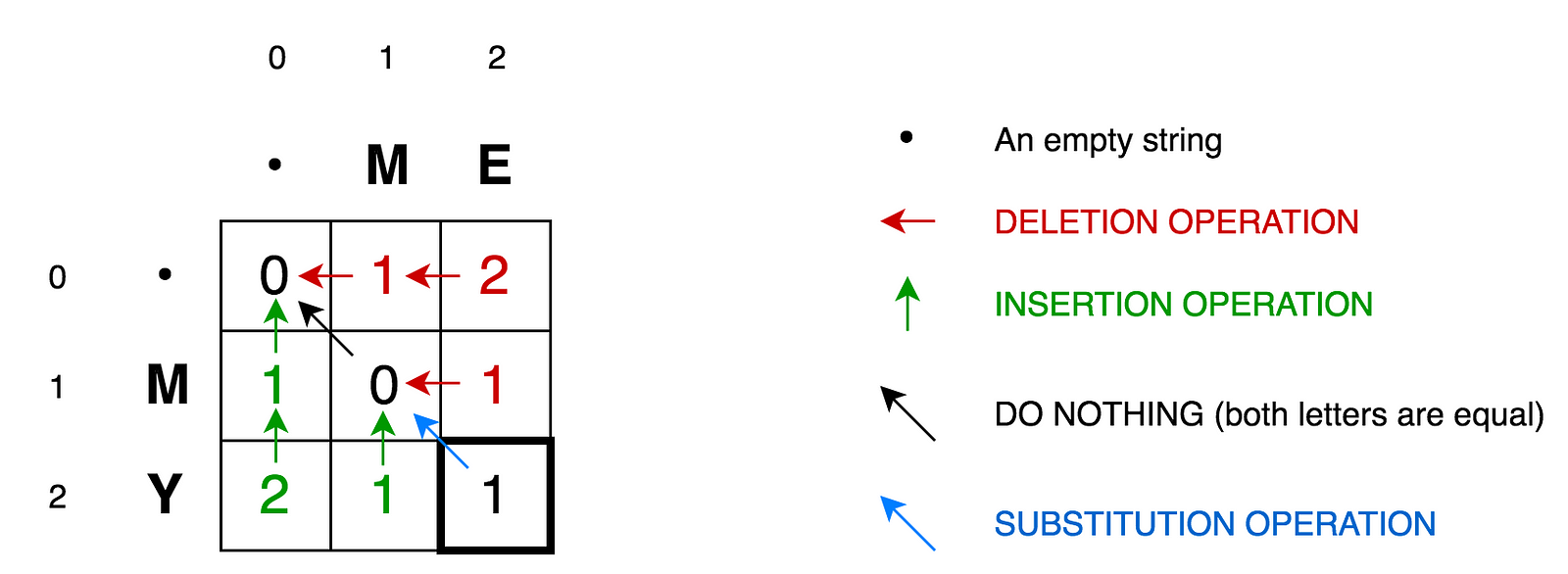 |
| 69 | + |
| 70 | +- Cell `(0:1)` contains red number 1. It means that we need 1 operation to |
| 71 | + transform `M` to an empty string. And it is by deleting `M`. This is why this number is red. |
| 72 | +- Cell `(0:2)` contains red number 2. It means that we need 2 operations |
| 73 | + to transform `ME` to an empty string. And it is by deleting `E` and `M`. |
| 74 | +- Cell `(1:0)` contains green number 1. It means that we need 1 operation |
| 75 | + to transform an empty string to `M`. And it is by inserting `M`. This is why this number is green. |
| 76 | +- Cell `(2:0)` contains green number 2. It means that we need 2 operations |
| 77 | + to transform an empty string to `MY`. And it is by inserting `Y` and `M`. |
| 78 | +- Cell `(1:1)` contains number 0. It means that it costs nothing |
| 79 | + to transform `M` into `M`. |
| 80 | +- Cell `(1:2)` contains red number 1. It means that we need 1 operation |
| 81 | + to transform `ME` to `M`. And it is by deleting `E`. |
| 82 | +- And so on... |
| 83 | + |
| 84 | +This looks easy for such small matrix as ours (it is only `3x3`). But here you |
| 85 | +may find basic concepts that may be applied to calculate all those numbers for |
| 86 | +bigger matrices (let’s say a `9x7` matrix for `Saturday → Sunday` transformation). |
| 87 | + |
| 88 | +According to the formula you only need three adjacent cells `(i-1:j)`, `(i-1:j-1)`, and `(i:j-1)` to |
| 89 | +calculate the number for current cell `(i:j)`. All we need to do is to find the |
| 90 | +minimum of those three cells and then add `1` in case if we have different |
| 91 | +letters in `i`'s row and `j`'s column. |
| 92 | + |
| 93 | +You may clearly see the recursive nature of the problem. |
| 94 | + |
| 95 | +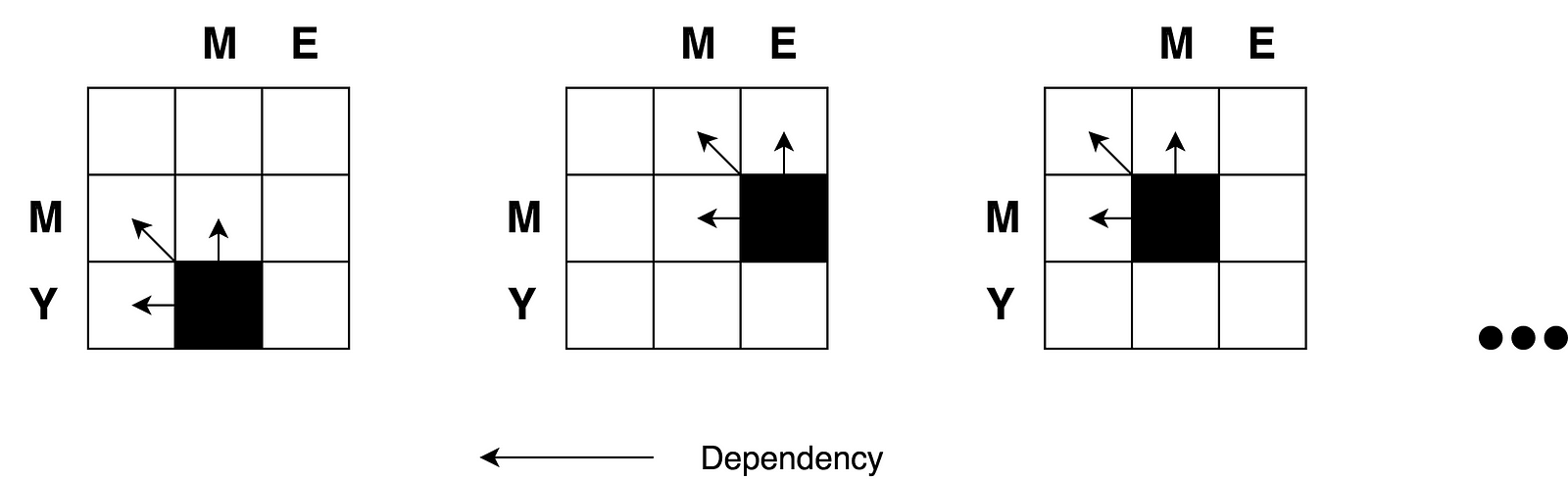 |
| 96 | + |
| 97 | +Let's draw a decision graph for this problem. |
| 98 | + |
| 99 | +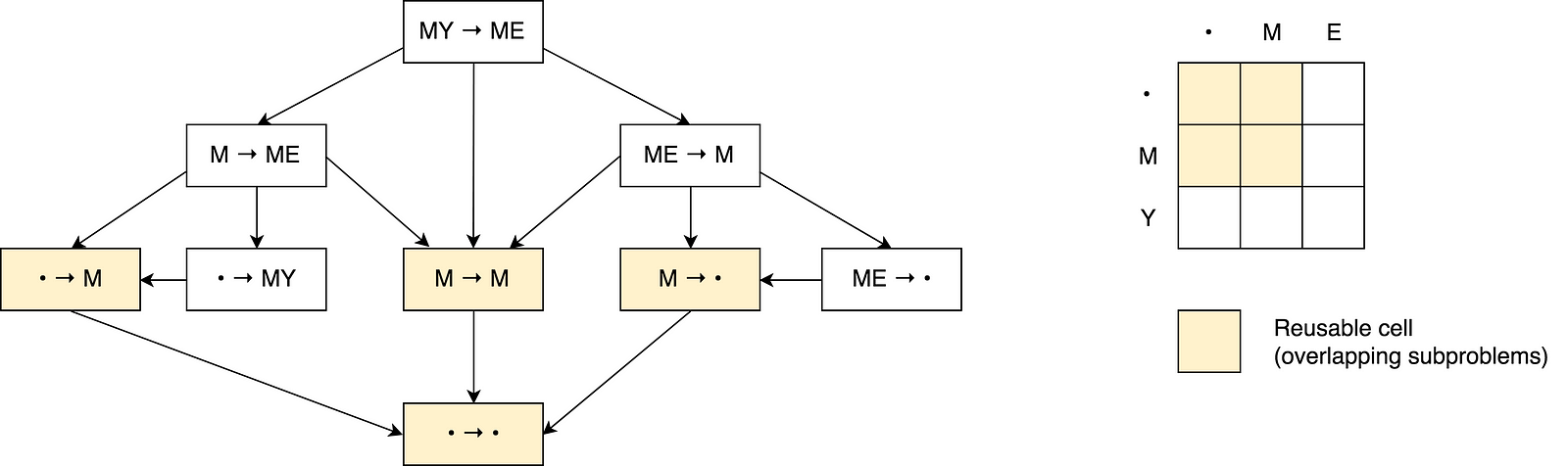 |
| 100 | + |
| 101 | +You may see a number of overlapping sub-problems on the picture that are marked |
| 102 | +with red. Also there is no way to reduce the number of operations and make it |
| 103 | +less than a minimum of those three adjacent cells from the formula. |
| 104 | + |
| 105 | +Also you may notice that each cell number in the matrix is being calculated |
| 106 | +based on previous ones. Thus the tabulation technique (filling the cache in |
| 107 | +bottom-up direction) is being applied here. |
| 108 | + |
| 109 | +Applying this principle further we may solve more complicated cases like |
| 110 | +with `Saturday → Sunday` transformation. |
| 111 | + |
| 112 | +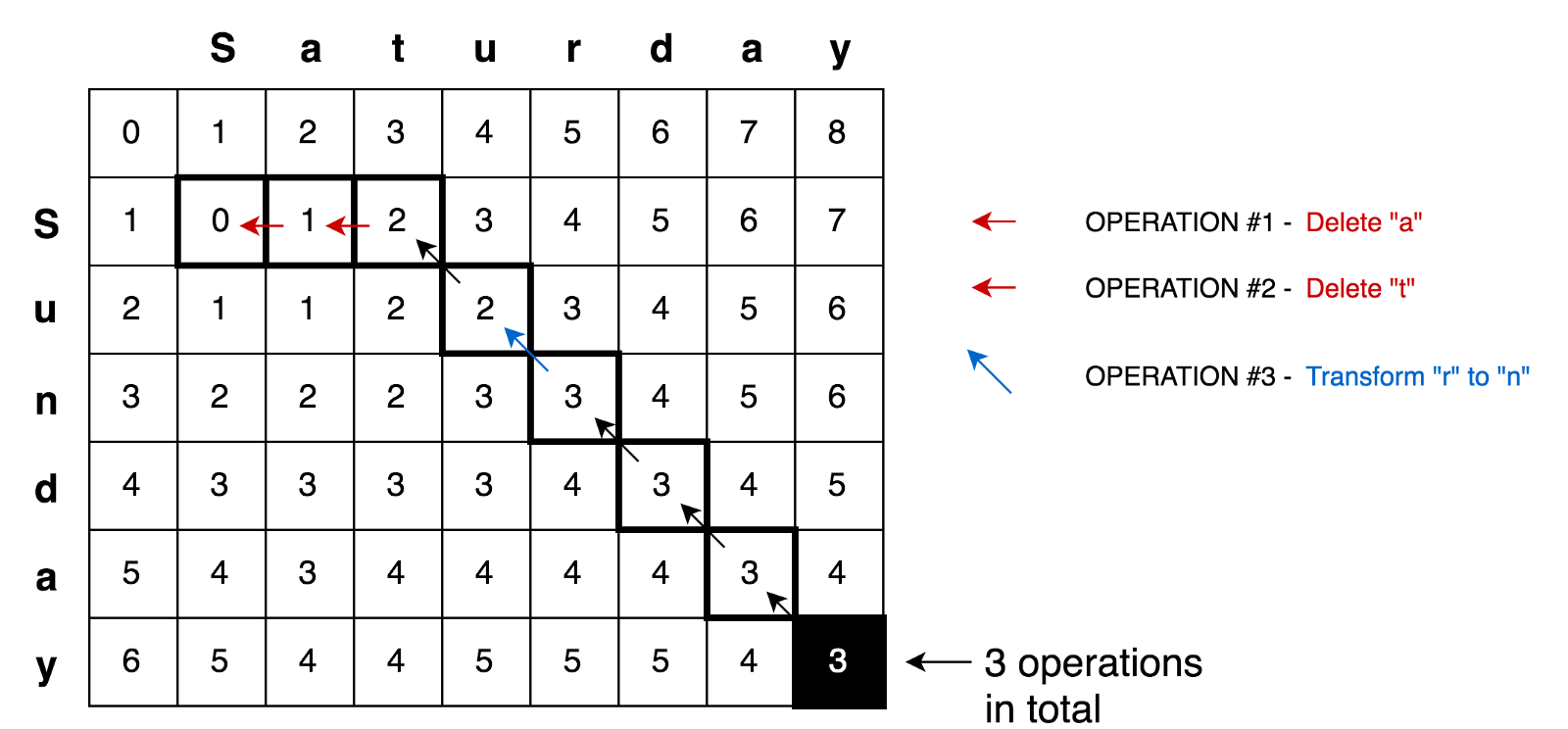 |
| 113 | + |
| 114 | +## References |
| 115 | + |
| 116 | +-[Wikipedia](https://en.wikipedia.org/wiki/Levenshtein_distance) |
| 117 | +-[YouTube](https://www.youtube.com/watch?v=We3YDTzNXEk&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) |
| 118 | +-[ITNext](https://itnext.io/dynamic-programming-vs-divide-and-conquer-2fea680becbe) |
0 commit comments